|
Blueprints for this Lesson: |
|
 Foundational Knowledge:
Foundational Knowledge:
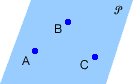
Draw four points on a piece of paper in your notebook. How many straight lines can you draw through these points?
Roll your cursor over the image below to see the solution.
 When you see this symbol, be sure to click on it as it will provide you with helpful information.
When you see this symbol, be sure to click on it as it will provide you with helpful information.
What do you think of when you read the title to this lesson, Building Blocks of Geometry? Take a moment and make a list of what you think these building blocks are.
In your list, did you mention points, lines and planes? If you did, you are right! But what exactly are these things?
Framework for Understanding:
In geometry, the terms point, line, and plane are referred to as undefined. When you write the definition of these terms, you must rely on other terms that need defining. Because of this, mathematicians use a general description of their meanings instead of a formal definition.
Point
|
In general, a point
is a location. Since points have no size, we say they have no
dimension. Points are named using a capital letter. The point to the left is point A. |
Television screens, computer monitors, and graphic calculator displays are examples of points as tiny dots, called pixels. A combination of pixels creates the pictures you see, and your picture will have better resolution with more pixels. When marching bands spell out words, each person in the band represents one point (dot) of a letter, acting as one of many pixels that creates an image.
Line |
A line can be described as a "stream" of points which has no width or depth. Since we can measure the distance between points, we say lines have one dimension: length. Lines can be named using two or more points on the line or using a
lower case script letter. The line to the left can be named Points that lie on the same line are called collinear. |
Throughout this course, you will learn many postulates and theorems that are very important in geometry. A postulate is a statement that is accepted as true without proof. A theorem is a statement that has been proven. It is important that you record these two definitions in your Geometry notebook, along with your other notes, definitions, and examples.
Postulate 1
Through any two points, there is exactly one line.
Postulate 2
A line contains at least two distinct points.
Plane
|
A plane is a flat surface that extends
indefinitely in all directions. Since we can make two measurements
on a plane, the distance between two points on a line and the distance
from a line to a point not on that line, we say planes have two
dimensions: length and width.
A plane can be named using three noncollinear points inside the plane
or using a script capital letter. The plane to the left can be called
plane
Points that lie in the same plane are called coplanar. Points that do not line in the same plane are called noncoplanar. |
| There are several postulates that apply to planes. | |
Postulate 3
Through any three noncollinear points, there is exactly one plane.
Postulate 4
A plane contains at least three noncollinear points.
Postulate 5
If two distinct points lie in a plane, then the line joining them lies
in that plane.
Postulate 6
If two distinct planes intersect, then their intersection is a line.
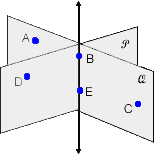
Plane  and
and 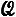 intersect to form
intersect to form ![]() .
.
In geometry, the set of all points is called space. Imagine the inside of a box. The bottom of the box is part of a plane and the area above it consists of infinitely many points. Since we can now make three measurements, the length and width of the plane and the height of the points above the plane, we say that space has three dimensions: length, width, and height (or depth).
It is important to incorporate mathematical terminology when writing. In this course the theme is architecture. The undefined terms of Geometry (point, line and plane) can be used to describe many parts of a building or room. Look at the diagram below:

What undefined term would best describe the entire floor? Yes, it would be a plane. How about the side of one of the dark shapes? Does it look more like a line or a plane? It is easy to use your prior experiences to know that this is a line. Finally, what undefined term would best represent the tip where the light and dark shapes meet? This would most definitely be a point.
Write a three sentence paragraph describing the room you are currently in. Your paragraph must include the three undefined terms of Geometry. You will be submitting your paragraph as part of the assessment for lesson 1.02.
Follow the links below to learn more about points, lines, planes, and space.
Move on to the Practice tab at this time.



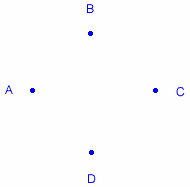
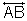 or line
or line