 |
Blueprints for this Lesson: |
|
 Foundational Knowledge:
Foundational Knowledge:
An angle is a figure consisting of two rays with a common endpoint.
Angles are made up of two main parts:
- Two sides formed by rays.
- The common endpoint where the two rays meet is called the vertex.
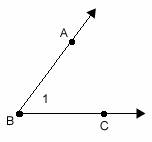
Sides:  and
and 
Vertex: point B
There are several ways to name this angle.
- Using three letters:
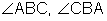
Notice that the vertex is always listed in the middle of the three letters. - Using one letter:
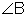
- Using a number:
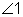
Framework For Understanding:
Have you ever looked at a structure to determine why it was pleasing to the eye? If you have, perhaps you noticed that some types of angles provide a more pleasing structure. Did you know that the more pleasing structure may have a higher cost? Some types of angles are not generally used in places where support is needed and therefore the architect must reinforce those angles with more expensive materials. Let's look closely at the types of angles and how we name them in Geometry.
| Perpendicular Lines | ||
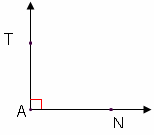
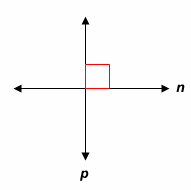
When two lines form to make right angles, we call them perpendicular. We use a symbol that looks like an upside down" T " for the word perpendicular. If : Then :
|
 |
|
In the image to the right, line n is perpendicular to line p.
|
 |
|
| Reminders | ||
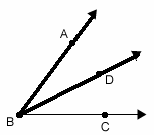
If more than one angle is formed at any vertex point, it is important that you name the angle using three letters, not just one.
|
 |
|
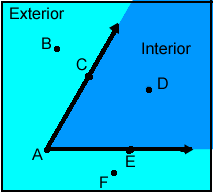
An angle divides a plane into three distinct parts:
|
 |
|
Take a few minutes and go on a Dynamic Exploration of Angles. Follow the directions on the page to explore different types of angles.
Now you are ready to move on to some practice with angles.



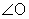 < 90°
< 90° 
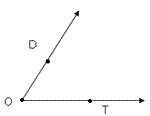
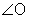 ,
,  , or
, or  .
.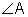 = 90°
= 90°
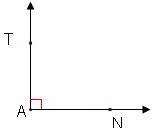
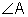 ,
, 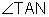 , or
, or 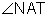 .
.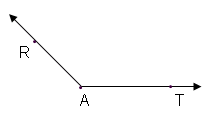
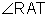 , or
, or  .
.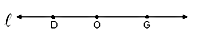
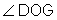 , but you will typically see it as line
, but you will typically see it as line 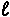 or
or 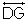 .
.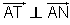
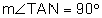
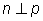
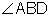 or
or 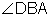 , but could not be named
, but could not be named 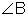 because vertex B belongs to more than one angle.
because vertex B belongs to more than one angle.


