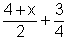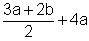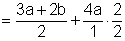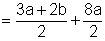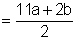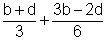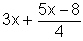| Blueprints for this Lesson: |
|
Simplifying Algebraic Expressions:
Recall that to simplify an algebraic expression, you must have a common denominator.
| Examples: | ||
| 1. |
|
the least common denominator (referred to as LCD) is 4 |
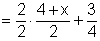 |
multiply the first expression by 2 | |
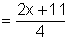 |
now combine like terms | |
| 2. |
|
|
| Simplify the following: | |
| 1. |
|
| 2. |
|
Verification of the Midpoint Formula:
Two of the topics that you learned about in this lesson were the Midpoint Formula and the Distance Formula.
According to the Midpoint Formula, the midpoint of 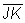 has coordinate has coordinate 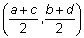 . . Let’s verify that this is the midpoint of 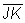 by using the Distance Formula to show that JM = KM. Try to work out the problem as we go through the process step-by-step. by using the Distance Formula to show that JM = KM. Try to work out the problem as we go through the process step-by-step. |
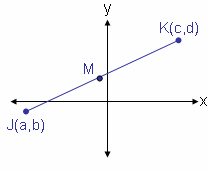 |
Given: M is the midpoint of 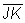 ,
with J(a, b), K(c, d), and JM
,
with J(a, b), K(c, d), and JM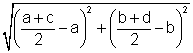
Prove: JM = KM
Using the distance formula, we will first find the value of JM.
1. JM = 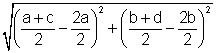 |
1. Substitute the values of J and M into the distance formula. |
2. JM = 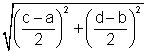 |
2. The LCD for the expressions is 2. |
3. JM = 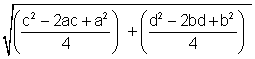 |
3. Collect like terms. |
4. JM = 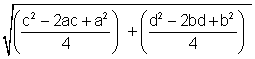 |
4. Recall that 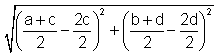 means
means 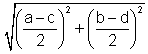 . .Now multiply (c-a)(c-a) and (2)(2), then collect like terms. |
We will repeat the process to find the value of KM. Try this one on your own and then click on each step to check your work.
Since JM = KM = 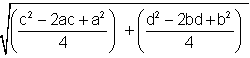 , we have verified that M is the midpoint of
, we have verified that M is the midpoint of 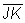 .
.
Derivation of the Pythagorean Theorem:
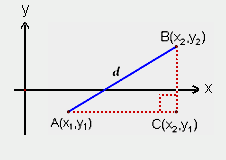
| In this lesson, you reviewed the process of using the Pythagorean Theorem to find the distance between two points. Now we are going to derive the Distance Formula using the Pythagorean Theorem. |
To find the distance from A to B, first we will need to find AC and BC.
AC = |x2 - x1| This is the horizontal distance from A to C.
BC = |y2 - y1| This is the vertical distance from B to C.
According to the Pythagorean Theorem,
hypotenuse2 = leg2 + leg2 |
|
| (AB)2 = (AC)2 + (BC)2 | Substitute the sides into the formula. |
| d2 = |x2 - x1|2 + |y2 – y1|2 | Substitute the lengths of each side. |
| d2 = (x2 - x1)2 + (y2 – y1)2 | Any value squared is positive, so we can remove the absolute value signs. |
d = 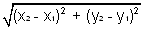 |
Since distance is positive, d must also be nonnegative. |
This leads to the Distance Formula that you viewed in the lesson.
Distance Formula Given the points (x1, y1) and (x2, y2), the distance between the two points is found using the following formula: |
You are now ready to go the assessment area of your course and submit "1.05H Segments and the Coordinate Plane."