 |
Blueprints for this Lesson: |
|
 Foundational Knowledge:
Foundational Knowledge:
Simplify the following:
- 52
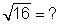
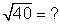
- (4 - 7)2 + (-2 - 8)2
 Click
here to check your answers.
Click
here to check your answers.
Framework for Understanding:
Imagine you are planning to build a home on a piece of property. Do you
think you might want to use graph paper in some way? Would you want to
know the size and location of the property for the home before you started?
Of course! This information would help you design the home to meet building
requirements for that property. The graph paper would help you map out
the exact measurements and location before you started.
In math, we often use a coordinate plane to draw figures and to provide
locations for them. It is important that you are able to read coordinates
and know how to graph them. In this lesson you will review how to graph
ordered pairs (coordinates), learn how to use a coordinate plane to
measure distance, and find the midpoints of segments.
The Coordinate Plane - Web Interactivity
Read through the following interactive lesson. It is important that you
are comfortable with the parts of the coordinate plane, how to graph ordered
pairs, and how to name points.
- Go to the SAS® Curriculum Pathways®.
- You will be asked for a user name and password. Visit the materials
list in the Course Information area for this information.
- Find the Quick Launch box. Type in the Web Inquiry number 963.
- Click Go. You can also locate activities by subject and title.
- When a new screen is displayed, click on "Coordinate Plane" on the
Graphers menu.
- A new screen will be displayed. You can use the given ordered pairs or type in
your own ordered pairs. (You can also move the existing ordered pairs.)
- There are four check boxes under the "graph paper" on the right of the screen. Click on
Label all points and Show quadrants to see these items illustrated in
the graph.
- Click on "Practice" on the left of the screen, to practice plotting points
given the ordered pairs (Part 1) and identifying the ordered pairs given
graphed points (Part 2).
Distance Formula:
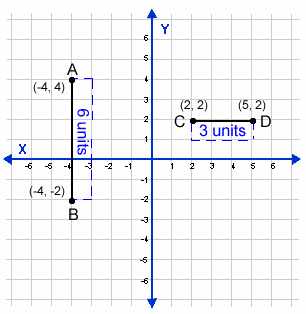
When two points are graphed on a coordinate plane, it is important that
you can find the distance between them. Sometimes this process is easy,
because the two points are on the same vertical or horizontal line. Look
at the examples below. 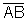 is a vertical segment. It is easy to use the y-axis as a number line and
determine the length of the segment.
is a vertical segment. It is easy to use the y-axis as a number line and
determine the length of the segment.  is a horizontal segment. You can use the x-axis as a number line and determine
the length of the segment. Roll your cursor over the image to see the
lengths of each segment.
is a horizontal segment. You can use the x-axis as a number line and determine
the length of the segment. Roll your cursor over the image to see the
lengths of each segment.
Not all segments graphed on a coordinate plane are vertical or horizontal. Some are diagonal. Because these segments do not follow a number line, we have to do more than just count boxes to determine their length. Mathematicians have devised a distance formula to be used in this situation. To see the derivation of this formula (where it came from) click here.
Distance Formula Given the points (x1, y1) and (x2,
y2), the distance between the two points is found using
the following formula: |
|
|
|
| Example 1: | |
| Find the distance between the ordered pairs (5, 8) and
(3, -2). x 1 = 5 x2 = 3 y1 = 8 y2 = -2 |
Step 1: Determine the values for x1,
y1, x2, and y2 before you begin.
Note: The values of x1 and y1 are the x and y values from the first ordered pair. The values of x2 and y2 are the x and y values from the second ordered pair. |
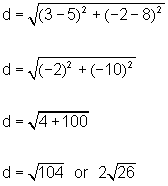
|
Step 2: Substitute the values for x1, y1, x2, and y2 into the distance formula and simplify according to the order of operations. |
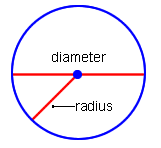
| In order to understand this next example, please review the following important information about circles. | |
|
|
| Example 2: | |
| What is the length of the radius that connects the point
(-1, 3) on the circle to the center point (2, 8)? x1 = -1 x2 = 2 y1 = 3 y2 = 8 |
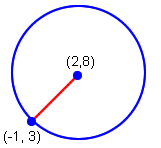
Step 1: Determine the values for x1, y1, x2, and y2 before you begin.
|
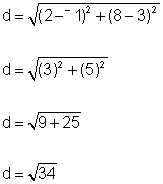
|
Step 2: Substitute the values for x1, y1, x2, and y2 into the distance formula and simplify according to the order of operations. |
Midpoint Formula Given the points (x1, y1) and (x2,
y2), the midpoint between the two points is found using
the following formula: Notice: The midpoint is an actual ordered pair. |
|
The midpoint formula allows us to find the midpoint between two points on a line segment. |
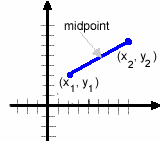
|
| Example 3: | |
| Find the midpoint between the points (-2, 2) and (6,
4). x1 = -2 x2 = 6 y1 = 2 y2 = 4 |
Step 1: Indentify the values for x1,
y1, x2, and y2 before you begin.
|
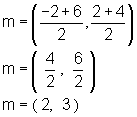 |
Step 2: Substitute the values for x1, y1, x2, and y2 into the midpoint formula and simplify following the order of operations. |
| Example 4: | |
The midpoint of 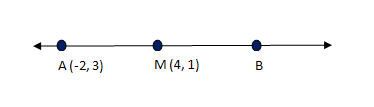 |
|
x-coordinate of M= 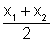 |
y-coordinate of M= 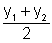 |
| x-coordinate of M=4 y-coordinate of M=1 x1 = -2 y1 = 3 |
Step 1: Identify the values for x1, y1, x2, and y2 before you begin. |
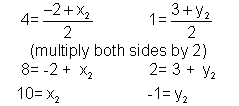
|
Step 2: Substitute the values for the x and y-coordinates of M, x1, y1, and simplify. |
| Endpoint B has coordinates (10, -1) | Step 3: Write the coordinates as an ordered pair. |
Move on to the practice page to try some on your own.




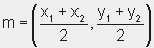
 is M (4, 1). One endpoint is A (-2, 3). Find the coordinate
of the other endpoint B.
is M (4, 1). One endpoint is A (-2, 3). Find the coordinate
of the other endpoint B. 

