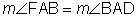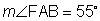 |
Blueprints for this Lesson: |
|
Foundational Knowledge:
- Draw and label a figure that represents the following information:
- Points B, C and D are collinear and C is between B and D.
- BC = 2x + 4
- CD = 4x - 8
- If BD = 32, find BC and CD.
- What can you say about point C in relationship to points B and D?
Click here to check your answers.
Framework for Understanding:
Do you think architects ever have to solve problems related to angles? For example, would they ever have different angles coming together to make a larger angle? Would they ever have to figure out how to cut an angle exactly in half?
Earlier you learned all about different types of angles and how to classify them. Now, let’s take a look at some foundational concepts concerning angles and how to use those concepts to solve problems.
Postulate 9 – Angle Addition Postulate
If point D is in the interior of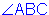 
, then m
+ m
= m.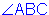
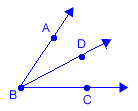
This postulate tells us that if you have two angles that share a side (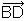
), then the measures of the smaller angles will add up to the measure of the larger angle. You can use this information to solve problems for missing angle measures.
Example 1:
Find m
if 
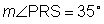and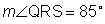 
.
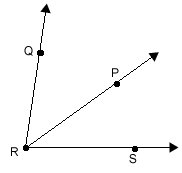
Step 1: Label the parts of the figure.
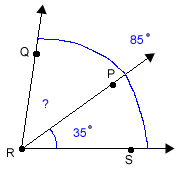TIP: The key to solving many problems in Geometry is drawing the figure and labeling the parts. This will help you identify relationships among the parts of the figure.
In this example, we know the smaller angles add up to 85 degrees and we know that one of the angles is 35 degrees. How can we find the other angle?
Step 2: Look for relationships between the parts of the figure that can be used to set up an equation.
Using the angle addition postulate, we can set up an algebra equation that will help us solve for the missing angle. You can call the missing angle x.
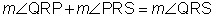
Step 3: Solve for x.
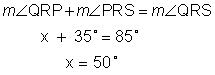
Step 4: Answer the question.
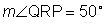
Step 5: Check your answer.
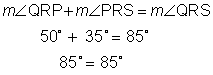
Let’s try another one using algebraic expressions instead of numbers for the angles. Does the process still work? Sure it does!
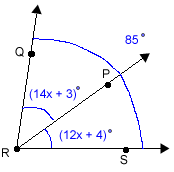
Example 2:
Use the following information to solve for x and then find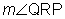 
and m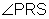 
.
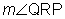= 14x + 3
m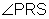= 12x + 4
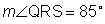
Step 1: Label the parts of the figure.
In this example, we know the smaller angles add up to 85 degrees.
Step 2: Look for relationships between the parts of the figure that can be used to set up an equation.
Step 3: Solve for x.
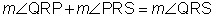
(14x + 3) + (12x + 4) = 85
26x + 7 = 85
26x = 78
x = 3
Step 4: Answer the question.
= 14(3) + 3
= 42 + 3
m
= 12(3) + 4
= 36 + 4
m
Step 5: Check your answer.
45° + 40° = 85°
Your work here with the angle addition postulate probably reminded you of the work you did earlier in the course with the segment addition postulate. Do you remember that lesson? In that same lesson, you also learned about the midpoint of a segment. It is the point where the segment is divided into two congruent parts. In an angle, the ray that divides the angle into two congruent parts is called the angle bisector. You can use the definition of an angle bisector to find the measures of angles.
Example 3:
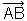bisects 
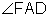so that 
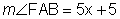and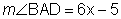 
. Solve for x and find 
.
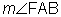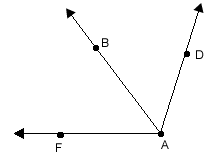
Step 1: Label the parts of the figure.
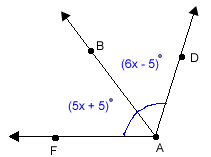In this example, we are told that 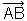bisects 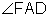. This means the two smaller angles that make up 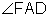are congruent.
Notice the congruent angle marks on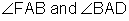 
.
Step 2: Look for relationships between the parts of the figure that can be used to set up an equation.
Using the definition of angle bisector, we can write an equation where.
Step 3: Solve for x.
(5x + 5) = (6x – 5)
10 = x
Step 4: Answer the question.
= 5(10) + 5
= 50 + 5
Step 5: Check your answer.
(5x + 5) = (6x – 5)
5(10) + 5 = 6(10) – 5
50 + 5 = 60 – 5
55 = 55
Important tip: It is important to remember that illustrations in Geometry are not always drawn to scale. In other words, items that appear to be the same size, may not be unless they are labeled as congruent.
It is time to move on for some practice with the angle addition postulate and angle bisectors.
