 |
Blueprints for this Lesson: |
|
 Foundational Knowledge:
Foundational Knowledge:
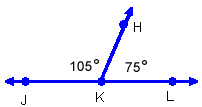
Use the information given in each figure to find the measure of the missing angle, labeled x.
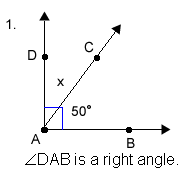
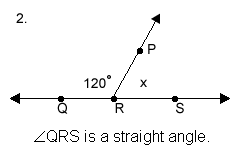
 Click here to check
your answers.
Click here to check
your answers.
Framework for Understanding:
You have learned many things about angles so far in this module. Now, let’s focus on the relationships between two angles, sometimes called angle pairs.
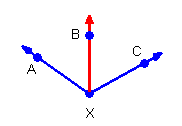 Two
angles that share a side are called adjacent
angles.
Two
angles that share a side are called adjacent
angles.
 are adjacent angles because they share
are adjacent angles because they share  It is important
to know that while
It is important
to know that while ![]() share side
share side ![]() they are not considered adjacent. This is because
they are not considered adjacent. This is because 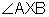 is part of
is part of 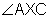 .
.
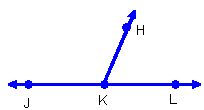 Two
angles that together form a straight angle are called a linear
pair.
Two
angles that together form a straight angle are called a linear
pair.
 are a linear pair.
are a linear pair.
 Two
angles that add up to 180 degrees are called supplementary
angles.
Two
angles that add up to 180 degrees are called supplementary
angles.
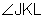 is
a straight angle that measures 180 degrees.
is
a straight angle that measures 180 degrees.  and
and  are called supplementary angles because their measures add up to 180 degrees.
are called supplementary angles because their measures add up to 180 degrees.
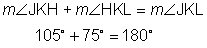
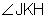 is the supplement of
is the supplement of 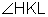 ,
and
,
and 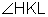 is the supplement of
is the supplement of 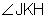 .
.
If supplementary angles are adjacent, then they are also called a linear pair. Supplementary angles do not have to be adjacent in order to be supplementary. As long as two angles add to be 180 degrees, they are supplementary. Here is another visual example.
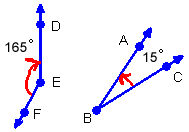
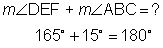
Because they add up to 180 degrees, 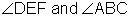 are supplementary.
are supplementary.
 Two
angles that add up to 90 degrees are called complementary
angles.
Two
angles that add up to 90 degrees are called complementary
angles.
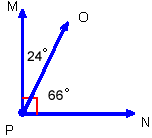
 is a right angle and measures 90 degrees. The two smaller angles that
make up
is a right angle and measures 90 degrees. The two smaller angles that
make up  are
are  .
They are called complementary angles because their measures add up to
90 degrees.
.
They are called complementary angles because their measures add up to
90 degrees.
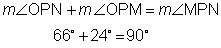
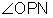 is the complement of
is the complement of 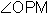 and
and 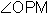 is the complement of
is the complement of 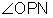 .
.
 Complementary
angles do not have to be next to one another to be complementary. As long
as two angles add to be 90 degrees, they are complementary. Here is another
visual example.
Complementary
angles do not have to be next to one another to be complementary. As long
as two angles add to be 90 degrees, they are complementary. Here is another
visual example.
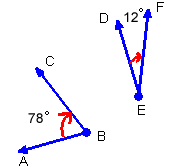
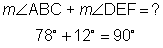
Because they add up to 90 degrees, 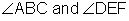 are complementary.
are complementary.
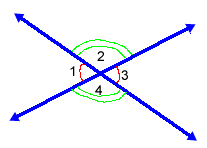 Two
non-adjacent angles that are opposite (across from) each other when two
lines intersect are called vertical angles.
Pairs of vertical angles are congruent.
Two
non-adjacent angles that are opposite (across from) each other when two
lines intersect are called vertical angles.
Pairs of vertical angles are congruent.
You can use the angle pair relationships above to find measures of missing angles.
Example:
|
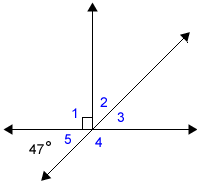
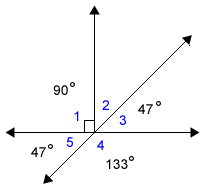
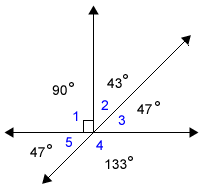
Use the given information to find the measures of all the angles in the figure. Given:
|
|
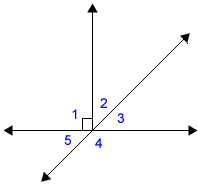
Step 1: Make a sketch of this figure on your own paper and label the measure of angle 5. |
|
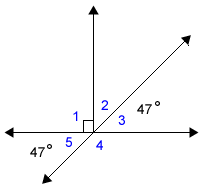
Step 2: Use the angle pair relationships to find the measures of the other missing angles. There are many ways to start this problem. You might see a different starting point, but eventually all the angle measures can be found. One starting point is to look for vertical angles in the illustration. Angle 5 and Angle 3 are vertical angles.
|
|
Angle 4 and angle 5 form a linear pair. That tells us they are supplementary angles and their measures must total 180 degrees.
We can use subtraction to figure out the measure of angle 4. 180 – 47 = 133 |
|
The measure of angle 1 is given in the drawing. It is a right angle.
|
|
There are several ways to find the measure of angle 2. Angles 1, 2 and 3 make a straight angle totaling 180 degrees. We know that angle 1 is a right angle measuring 90 degrees, so angles 2 and 3 combined must be another 90 degrees. Earlier we found the measure of angle 3 to be 47 degrees. So, if we subtract that from 90 degrees, we have 43.
|
|
Step 3: Answer the question. |
Example:
|
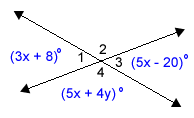
Use the given information to find the values of x and y. Find the measures of all four angles in this figure. |
||||||||||||
Before you get started, study the figure to identify any angle pair relationships. What do you know?
Does any of this information help you set up an equation to solve for x? |
|||||||||||||
We can write the following equation and solve for x. 3x + 8 = 5x – 20 Now, we can find the measures of angles 1 and 3.
|
|||||||||||||
Now that we know the value of x, and the measures of angles 1 and 3, we can find the measure of angle 4.
We have found everything except for the value of y. We know that (5x + 4y) must equal 130. This can be written as an equation. 5x + 4y = 130 Plug in x and solve for y.
The answer to this problem is a long one. |
|||||||||||||
Example:
The measure of an angle is 5 less than 4 times its complement. Find the measure of each angle.
If we let the angle be represented by x, then the complement = 90 –
x.
Now translate the sentence into an equation.
The measure of an angle
x |
is |
5 less than 4 times
its complement. 4(90-x) - 5 |
Now it is time to solve.
| x | = | 4(90-x) - 5 |
| x | = | 360 - 4x - 5 |
| x | = | 355 - 4x |
| 5x | = | 355 |
| x | = | 71 |
This means that the angle is 71° and its complement is 90 - 71 = 19°.
Move on to the practice page to apply what you have learned here.



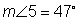
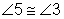
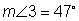
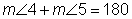
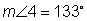
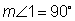
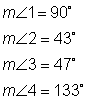
 1
and
1
and 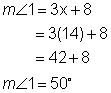
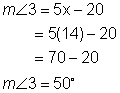
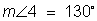
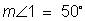 ,
,
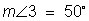 ,
,
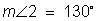 and
and


