 |
Blueprints for this Lesson: |
|
Foundational Knowledge:
Solving Systems of Equations
A set of equations with the same variables is called a system
of equations. A solution of a system of two equations with
two variables is an ordered pair that
makes both equations true.
In your Algebra 1 course, you were taught how to solve systems by the graphing method, substitution method, and elimination method. Let’s review two of those methods now.
Substitution Method
The objective of the Substitution Method is to solve for one of the variables
and substitute the expression into the other equation. Let's try this.
x + 2y = 10
3x + 4y = 8
Step 1: Solve for one of the variables in one of the equations. It is easier to solve for the variable that has a coefficient of 1. In our system of equations above, we will solve for the x in the first equation since it has a coefficient of 1.
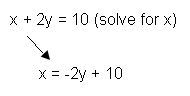
Step 2: Substitute the value of x into the other equation.
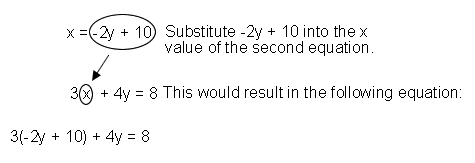
Step 3: Solve the equation to find the value of y.
3(-2y+10)+4y |
= |
8 |
-6y + 30 + 4y |
= |
8 |
-2y |
= |
-22 |
y |
= |
11 |
Step 4: Substitute the y value into one of the original equations, and then solve for x.
x + 2y |
= | 10 |
| x + 2(11) | = | 10 |
x + 22 |
= | 10 |
x |
= | -12 |
The solution to this system of equations is the point (-12, 11) .
This is the solution that will work in both equations.
Step 5: Check your solution. Remember that your solution must work in both equations.
| 1st equation: x + 2y | = 10 |
| -12 + 2(11) | = 10 |
| -12 + 22 | = 10 |
| 2nd equation: 3x + 4y | = 8 |
| 3(-12) + 4(11) | = 8 |
| -36 + 44 | = 8 |
Now you try one.
2x – y = 5
3y – x = 5
Click here to check
your answers.
Elimination Method
The objective of the Elimination Method is to create two equations that, when added together, will cancel out one of the variables. Let’s look at the equations from our first example.
| x + 2y | = 10 |
| 3x + 4y | = 8 |
If we multiplied the first equation by -3, then the x’s would cancel out when the equations are added together.
| 1st equation: -3(x + 2y) = -3(10) 2nd equation: 3x + 4y = 8 |
 |
Remember to multiply both sides of the equation by -3. |
| 1st equation: -3x – 6y = -30 2nd equation: 3x + 4y = 8 |
|
|
| -2y = -22 y = 11 |
|
Solve for y. |
All that is left now is to substitute y back into one of the original equations to solve for x just like you did in the Substitution Method.
| x + 2(11) | = | 10 |
x + 22 |
= | 10 |
x |
= | -12 |
The solution is (-12, 11)
Make sure to check that your solution (the ordered pair) works in BOTH equations.
Try the following on your own.
x – 3y = 0
5x – y = -14
Click here to check
your answers.
Framework for Understanding
Example 1:
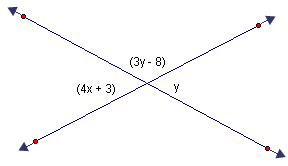
Notice that (3y – 8) and (y) form a linear pair, so their sum is 180.
Step 1: Solve for y.
| (3y - 8) + y | = | 180 |
4y - 8 |
= | 180 |
4y |
= | 188 |
y |
= | 47 |
Step 2: Solve for x by substituting.
| 4x + 3 | = | 47 |
4x |
= | 44 |
x |
= | 11 |
Solution: (11, 47)
Step 3: Check your answers.
| 3(47)-8+47 | =180 |
| 4(11)+3 | =47 |
Example 2:
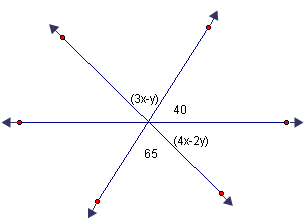
Notice that 65, (4x - 2y), and 40 form a straight angle, so their sum would be 180. (3x - y) and 65 are vertical angles, so their measurements are equal.
Therefore, the equations would be:
65 + (4x - 2y) +40=180 and
3x - y = 65
Step 1: Simplify:
| 65 + (4x - 2y) + 40 | = | 180 |
| 4x - 2y +105 | = | 180 |
| 4x - 2y | = | 75 |
Now the equations are:
4x - 2y = 75
3x - y = 65
Step 2: Multiply 3x - y = 65 by -2 so that the y's will cancel out.
| -6x + 2y | = -130 |
Step 3: Add the equations.
-6x + 2y = -130
4x – 2y = 75
-2x
= -55
x = 27.5
Step 4: Substitute to solve for y.
3(27.5) – y |
= | 65 |
82.5 – y |
= | 65 |
-y |
= | -17.5 |
y |
= | 17.5 |
Step 5: Check your work.
3(27.5) – 17.5 |
= | 65 |
65+[4(27.5)-2(17.5)]+40 |
= | 180 |
Try this on your own:
Angles J and K are complementary angles.
Angles Q and R are supplementary angles.
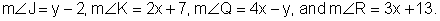
Find the values of x and y, and the measures of each angle.
Click here to check
your answers.
Remember to turn in your "1.09H Angle Relationships" assignment.
