|
Blueprints for this Lesson: |
|
 Foundational Knowledge:
Foundational Knowledge:
Try these on your own paper, and check your work with the answer link below.
Simplify the following:
- |-3|
- |-2 + 5|
- |-4 - 7|
Solve for x:
- 2x + 8 = -14
- x - 5 = 3x - 13
 Click
here to check your work.
Click
here to check your work.
Framework For Understanding:
Can you imagine drawing up a set of blueprints for a building and not using at least one segment in the drawing? It would be almost impossible. Everything would have to be made with arcs or circles. Think about how many geometric shapes are created using segments. So, whether you are working on a building or on a geometry problem, it is very important that you know everything you can about segments.
Finding the Lengths of Segments:
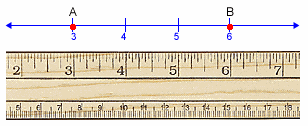
Find the distance between points A and B on the number line above. This is a lot like finding the length of something using a ruler.
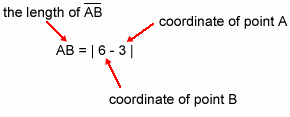
Did you notice the absolute value signs written around the | 6 - 3 |? These signs allow us to write the subtraction problem as 6 - 3 or 3 - 6. Either way, the absolute values will be the same and the answer will be the distance between the two points.
Postulate 7
On a ruler or number line, you can find the distance between two points by subtracting their coordinates and then taking the absolute value.
Segment Addition:
If three points are on the same line, then one point is between the other two. This is the definition of betweeness. This leads us to another postulate.
Postulate 8 - Segment Addition PostulateIf point C is between points A and B, then AC + CB = AB.

This postulate is helpful when we are trying to find missing information about lengths of segments.
Example: Q is between P and R with PQ = 2x - 1, QR = 3x + 5, and PR = 34. Write an equation to solve for x, then find PQ and QR. Make sure to check your solutions.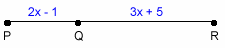
Before we can start solving this problem, we need to look at the illustration and identify some sort of equation. Because of the segment addition postulate, we know that PQ + QR = PR. Now that we have our equation, let's solve it.
| PQ + QR = PR (2x - 1) + (3x + 5) = 34 | Step 1: Replace PQ, QR and PR with
the given information.
|
||||||||||||||||||||||||||||||||
| Step 2: Solve the equation for x. | ||||||||||||||||||||||||||||||||
|
Step 3: Substitute the value of x into the expressions for PQ and QR and simplify. | ||||||||||||||||||||||||||||||||
| Solution: x = 6, PQ = 11 and QR = 23 | Step 4: Answer the question. | ||||||||||||||||||||||||||||||||
|
Check: PQ + QR = PR 11 + 23 = 34 |
Step 5: Check your solution. Substitute the values of PQ and QR into the original equation to verify your answer. |
Midpoint:
What do you think the term "midpoint" means? The word is made up of two
parts, "mid" and "point."
The midpoint of a segment
is the point that divides the segment into two equal parts. The midpoint
represents the middlemost point between two endpoints. Knowing this definition,
what type of equation can we set up to solve the following problem?
Example: Y is the midpoint of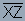 .
Find XY, YZ and XZ.
.
Find XY, YZ and XZ.
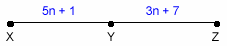
Because Y is given as the midpoint of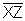 ,
we know that XY must equal YZ. In other words XY = YZ. Let's plug into
our equation what we know about XY and YZ and solve for n. Once we know
the value of n, we can find the measurements for XY, YZ and XZ.
,
we know that XY must equal YZ. In other words XY = YZ. Let's plug into
our equation what we know about XY and YZ and solve for n. Once we know
the value of n, we can find the measurements for XY, YZ and XZ.
|
Step 1: Replace XY and YZ with the
given information. XY = 5n + 1 YZ = 3n + 7 |
||||||||||||||||||||||||||||
|
Step 2: Solve the equation for n. | ||||||||||||||||||||||||||||
|
Step 3: Substitute the value of n into the expressions for XY and YZ and simplify. | ||||||||||||||||||||||||||||
| Solution: XY = 16, YZ = 16, XZ = 32 |
Step 4: Answer the question. | ||||||||||||||||||||||||||||
| Check:
XY = YZ 16 = 16 and XY + YZ = XZ 16 + 16 = 32 |
Step 5: Check your solution. Substitute the values of PQ and QR into the original equation to verify your answer. |
Now let's discuss other ways to cut a segment into two congruent parts.
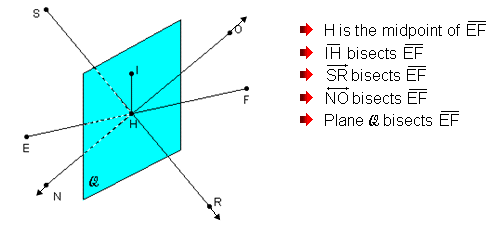
Segment Bisector:
A segment bisector is a segment, ray, line, or plane that intersects a segment at its midpoint.
It is time to move on and practice what you have learned.




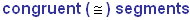 ?
?
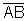 and
and 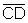 are equal, then
are equal, then 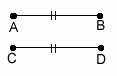 .
.