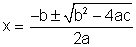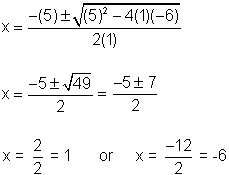skip navigation

lesson tab inactive practice tab inactive assignment tab inactive honors tab active

1.04 Segments

 

 Blueprints for this Lesson:
 
  • Review solving quadratic equations.
  • Review solving equations involving ratios.


Quadratic Equations:

Quadratic equations are written in the form ax2 + bx + c = 0. Two of the methods that can be used to solve quadratic equations are factoring and the quadratic formula. Let's review the process by working out a couple of examples. As you will see, either method will result in the same solutions.

Method 1: Factoring

x2 + 5x - 6 = 0

(x + 6)(x - 1) = 0

Note: If two factors multiply to equal zero, then one or both of the factors must equal zero. At this point, we can set each factor equal to zero and solve for x.

(x + 6)(x - 1) = 0
x + 6 = 0 or x - 1 = 0
x = -6 or x = 1


Check:

x
 = -6
(-6)2 + 5(-6) - 6
 = 0
36 + (-30) - 6
 = 0
or
    
x
 = 1
(1)2 + 5(1) - 6
 = 0
1 + 5 - 6
 = 0


Method 2: Quadratic Formula

For ax2 + bx + c = 0, a not equal to0,

The quadratic formula which states that x equals negative b plus or minus the square root of b squared minus 4 times a times c all being divided by 2 times a.

x2 + 5x - 6 = 0, where a = 1, b = 5, and c = -6. Now substitute into the quadratic formula above.

x equals negative 5 plus or minus the square root of 5 squared minus 4 times 1 times negative 6 all being divided by 2 times 1. This simplifies to x equals negative 5 plus or minus the square root of 49 all divided by 2 or negative 5 plus or minus 7 all divided by 2. The final solutions are x equals 1 and x equals negative 6.

Notice the solutions for x are the same whether you factored or used the quadratic formula to solve.

Method 1: Factoring

3x2 + 2x - 1 = 0
(3x - 1)(x + 1) = 0
3x - 1 = 0 or x + 1 = 0
x = 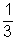one third or x = -1

Now make sure to check your solutions.
Method 2: Quadratic Formula

3x2 + 2x - 1 = 0,
where a = 3, b = 2,
and c = -1.
Now substitute into the quadratic equation.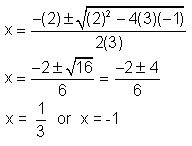

x equals -2 plus or minus the square root of 2 squared minus 4 times 3 times -1. This entire expression is over the expression 2 times 3. When it is simplified it becomes -2 plus or minus the square root of 16 all over 6. This simplifies to -2 plus or minus 4 all over 6. The solutions are x equals one-third or x equals -1.

Now it's your turn to solve. You may use either method.

  1. x2 - 6x + 8 = 0

  2. 2x2 = x + 10 (hint: remember to write it in the form ax2 + bx + c = 0)
check your work Click here to check your work


Solving Equations that involve Ratios:

Problems that involve ratios can be easily solved using an equation. Look at the following examples.

  1. A boy broke his teacher's yardstick into three pieces that are in a ratio of 2:3:4. How long is each piece? Solution: Write an equation using the variable x with each part of the ratio. Since a yardstick is 36 inches long, we know that the sum of the parts is 36 inches. The equation would look like this:
    2x + 3x + 4x = 36
    9x = 36
    x = 4; therefore the lengths are 2(4) = 8in., 3(4) = 12 in., and 4(4) = 16 in.
    Check your answer: 8 + 12 + 16 = 36

  2. A tree that was 56 feet tall was hit by lightning and is now in two pieces in a ratio of 3:4. Find the length of each piece.
    Solution:
    3x + 4x = 56
    7x = 56
    x = 8; therefore the lengths of the two pieces are 3(8) = 24 ft., and 4(8) = 32 ft.
    Check your answer: 24 + 32 = 56

Now you try one.
A is between C and T, and divides 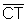line C Tinto a ratio of 3:7 respectively. If CT = 142 inches, find CA and AT.

check your work Click here to check your work



Go to the assessment area and submit your "1.04H Segments" assignment. This is in addition to submitting the regular "1.04 Segments" assignment.